原址：https://blog.csdn.net/silence2015/article/details/69063738

意义：图像视频只有被压缩才能有效大规模的存储和发送。

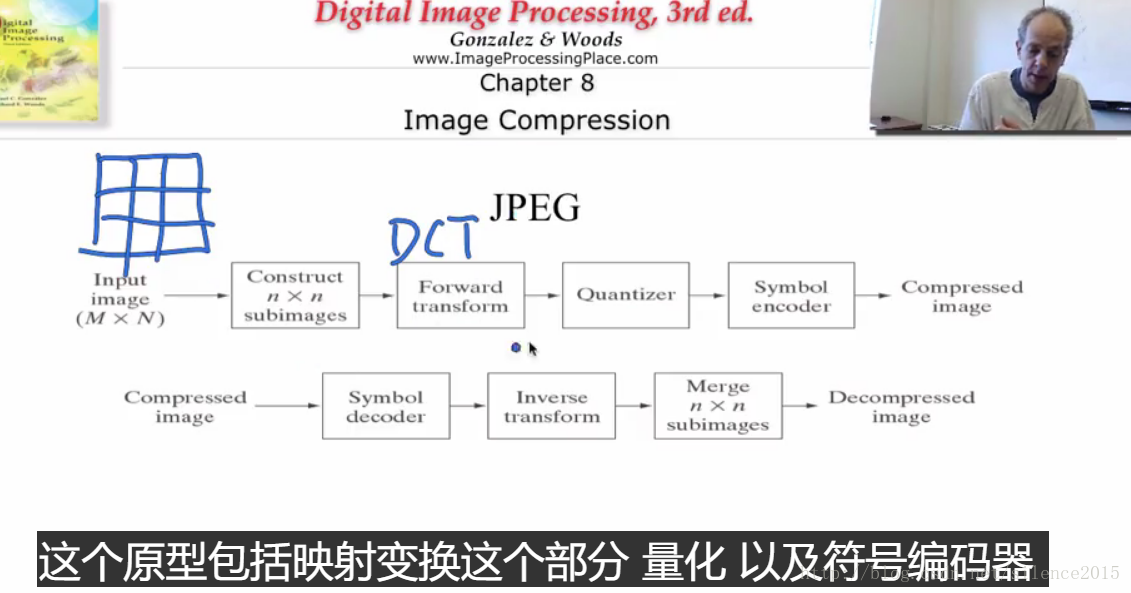
那么这儿总结我自己理解的图像压缩简单流程

压缩的方法论：我们首先做图像压缩是在频率域处理的，通过DCT（离散余弦变换）将图像转到频率域。低频部分也存储了图像的大多信息。我们知道，低频部分集中较多能量，含有图像大多平滑信息，而高频部分主要是边缘或者噪声。人眼对低频的光波比较敏感，故我们将高频部分合理丢掉部分，然后将频率域的图像进行量化处理，量化后的频率图像再进行编码处理，比如用哈夫曼编码来构造最短编码。通过编码后的图像就占用很少的一部分空间了。 

如需恢复图像，只需要指定相应的解码器来解码，再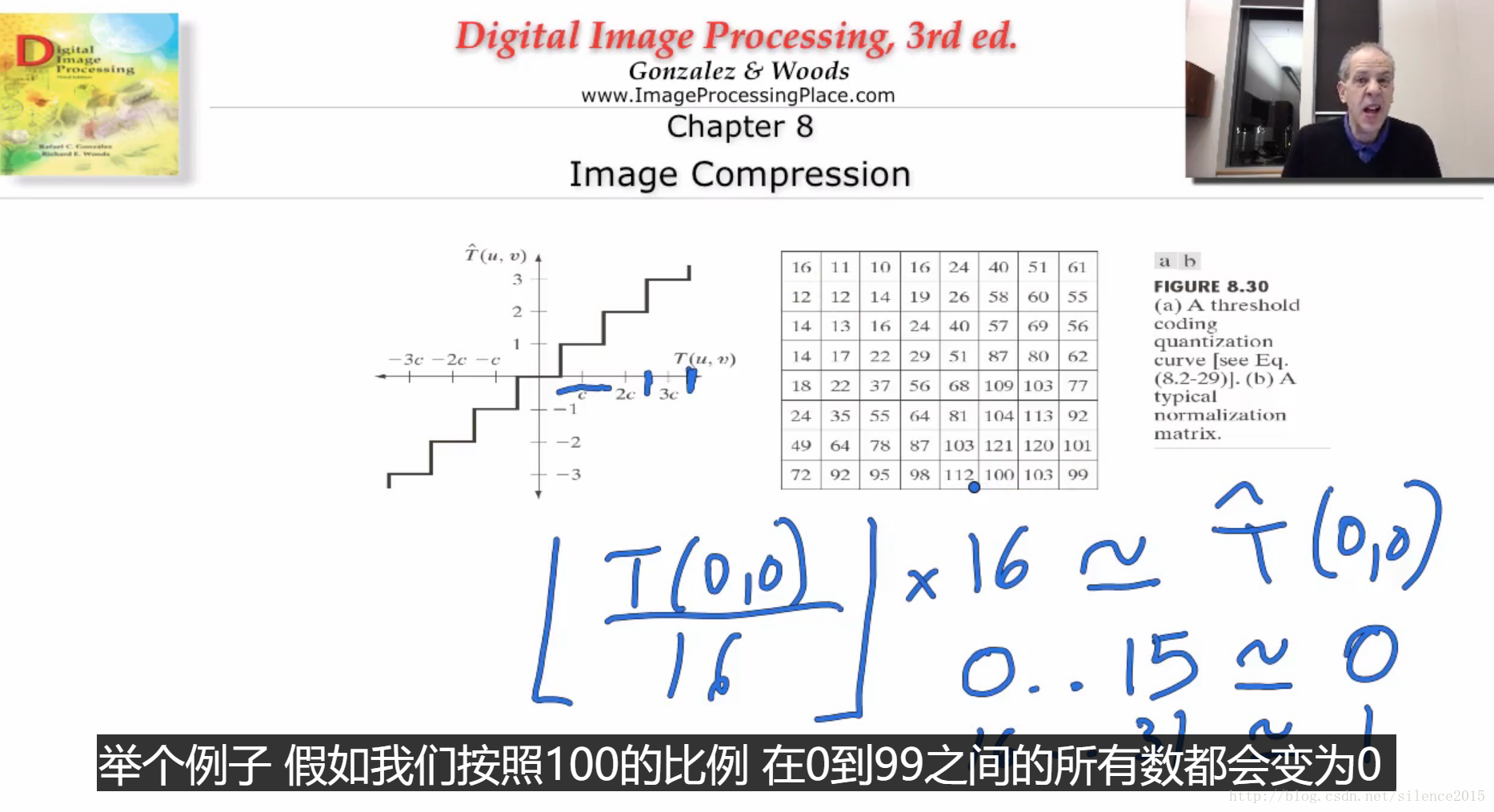

压缩过程： 

1、将图像分块，分成8*8 像素的小块来分别计算。 

2、对每个小块进行理算余弦变换，将图像转换到频率域。 

3、将图像量化，可通过量化矩阵（或者简单将每个像素除以N，取整，然后再乘以N，得到量化的目的，当然N越大，压缩的比率也就越大） 

4、通过合适的编码规则来对量化后的图像编码

解压过程： 

1、通过解码器将图像解码 

2、通过反变换（离散余弦反变换） 将图像从频率域转回空间域。 

3、合并所有8*8的小块

实验总结： 

1、为什么用DCT,而不用FFT？ 

因为DCT可以说少计算了复数，更方便计算

2、压缩损失主要在哪儿？ 

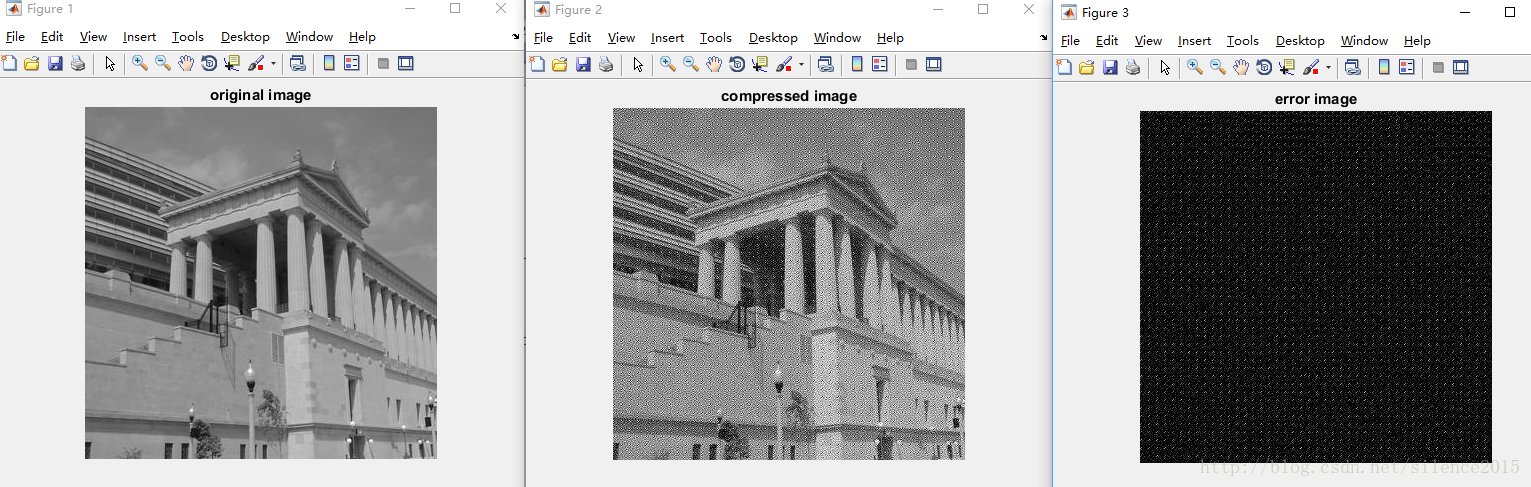
主要在量化的过程，图像做DCT变换只不过是一个从空间域到频率域的变换，并没有改变图像的属性。而量化的过程就是一个不断取整，保留大头，舍弃小的的过程。

function compressIMG(imgpath)    f=imread(imgpath);    %f=im2double(f);    f=double(f);    T=dctmtx(8);    dct=@(block_struct)T*block_struct.data*T';    invdct=@(block_struct)T'*block_struct.data*T;    f_tf=blockproc(f,[8,8],dct);    qt_mtx=[16,11,10,16,24,40,51,61;...        12,12,14,19,26,58,60,55;...        14,13,16,24,40,57,69,56;...        14,17,22,29,51,87,80,62;...        18,22,37,56,68,109,103,77;...        24,35,55,64,81,104,113,92;...        49,64,78,87,103,121,120,101;...        72,92,95,98,112,100,103,99];     % quantization     f_qt=blockproc(f_tf,[8,8],@(block_struct)block_struct.data./qt_mtx);     f_qt=ceil(f_qt);     % restore the image     g=blockproc(f_qt,[8,8],@(block_struct)block_struct.data.*qt_mtx);     g=blockproc(g,[8,8],invdct);     error=f-g;     f=uint8(f);     g=uint8(g);     error=uint8(error);     imshow(f),title('original image');     figure;     imshow(g),title('compressed image');     imwrite(g,'compressed_img.jpg');     figure;     imshow(error),title('error image');end

上面代码是我做的压缩实验，可以看出来效果并不理想。先往后学，以后再来提高。

参考资料：, 

最后致谢 Duke University

————————————–更新————————————–

经网友提示我复原得到的图的问题在于量化数值精度处理的问题，源代码中我用的f_qt=ceil(f_qt),ceil为向上取整，量化会造成数据丢失，使用round四舍五入可以完美解决这个问题f_qt=round(f_qt)。